Voraussetzung
Während der Erstellung der Matrix können wir auswählen, wie viele Minicodes jedem codierbaren Zeichen zugewiesen werden sollen.
📌 Praktisches Beispiel
Wenn wir eine Matrix mit 10 Minicodes erstellen, erhält jedes Zeichen 10 eindeutige und zufällige Minicodes.
Während der Codierung weist die Software jeder Vorkommen des jeweiligen Zeichens einen dieser Minicodes zu.
⚠️ Wichtig: Ein einzelner Minicode darf nur einmal verwendet werden.
🚫 Was passiert, wenn die Minicodes nicht ausreichen?
Wenn ein Zeichen im zu codierenden Text öfter vorkommt, als Minicodes vorhanden sind, schlägt die Codierung fehl.
✅ Beispiel:
Wir haben eine Matrix mit 10 Minicodes erstellt.
Wir wollen einen Text codieren, der 11 Buchstaben „c“ enthält.
❌ Die Codierung kann nicht abgeschlossen werden, da für das elfte „c“ kein Minicode mehr verfügbar ist.
Die Datei matrix.json
Um einen Text zu codieren, müssen wir zunächst sicherstellen, dass sich die Datei matrix.json der gewünschten Matrix im Arbeitsordner befindet.
Diese Datei ist für die Erstellung des Codes unerlässlich.
Codeerstellung
Im Abschnitt Text codieren klicken Sie auf Codieren.
Im sich öffnenden Fenster geben Sie den zu codierenden Text ein. Der Text kann sein:
- Manuell eingegeben.
- Per Copy-Paste eingefügt.
Sobald der Text eingegeben wurde, klicken Sie auf Bestätigen.
Das System erstellt automatisch den Code, der lokal im System gespeichert wird und im Arbeitsordner unter dem Namen code.txt sichtbar ist.
Wie die Kodierung funktioniert
Mit Cyphersol können jedem Großbuchstaben, Kleinbuchstaben, Akzentbuchstaben, Sonderzeichen, Zahl, Symbol, Leerzeichen und Zeilenumbruch verschiedene eindeutige Zufalls-Minicodes zugewiesen werden.
Wenn eine Matrix mit der Standardeinstellung (100 Spalten) erstellt wird, können jedem Zeichen bis zu 100 eindeutige Zufalls-Minicodes zugewiesen werden.
Bei der Matrixerstellung kann jedoch auch gewählt werden, bis zu 16382 Spalten zu erzeugen.
Der einem einzelnen Zeichen zugewiesene Minicode ist das Ergebnis einer Konkatenation.
Konkateniert wird der Inhalt einer beliebigen Zelle aus dem Bereich B mit den Zahlen der Zelle (zwingend aus derselben Spalte), die der Zeile des zu codierenden Zeichens entsprechen.
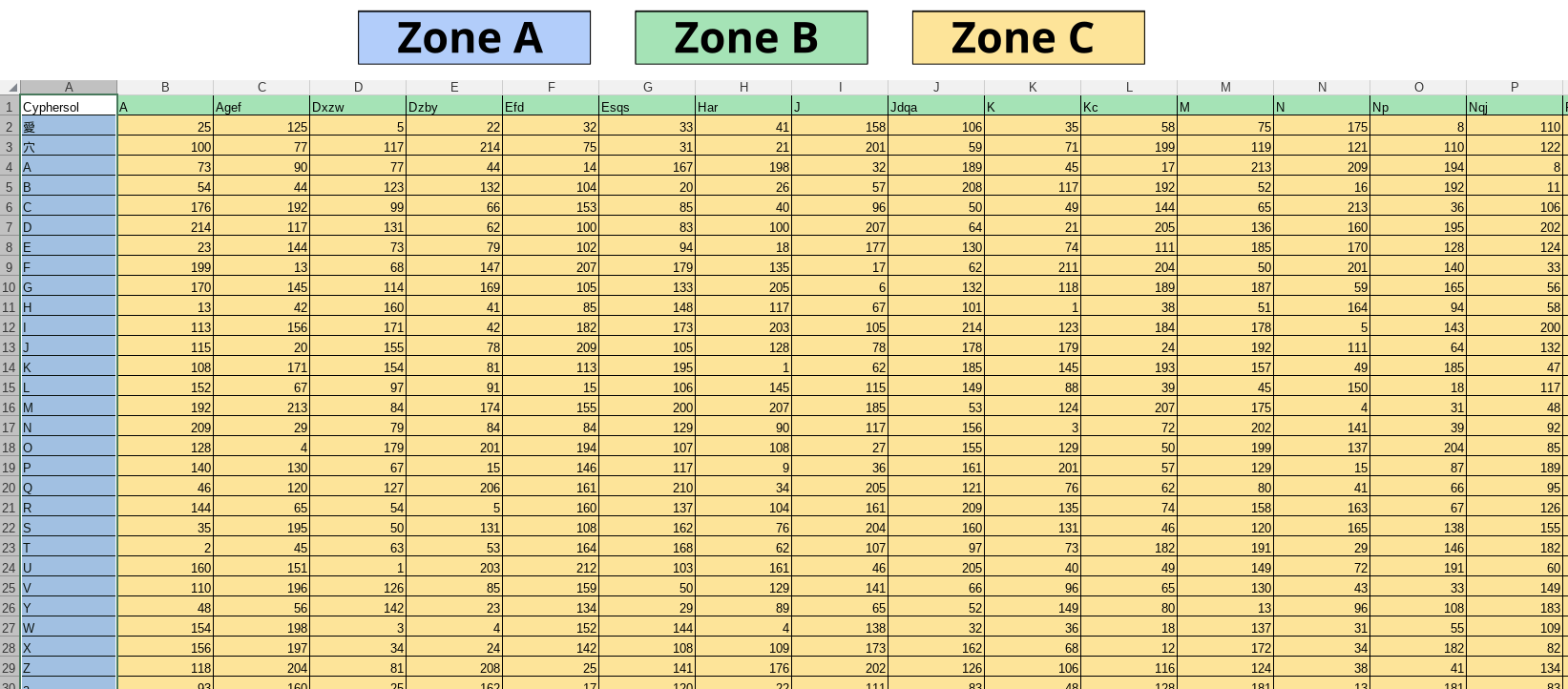
Beispiel einer Codierung basierend auf folgender Matrix:
Für dieses Beispiel verwenden wir den Matrixabschnitt aus diesem Bild, in dem wir nur die Großbuchstaben vollständig visualisieren können, da es sich um ein Bild handelt.
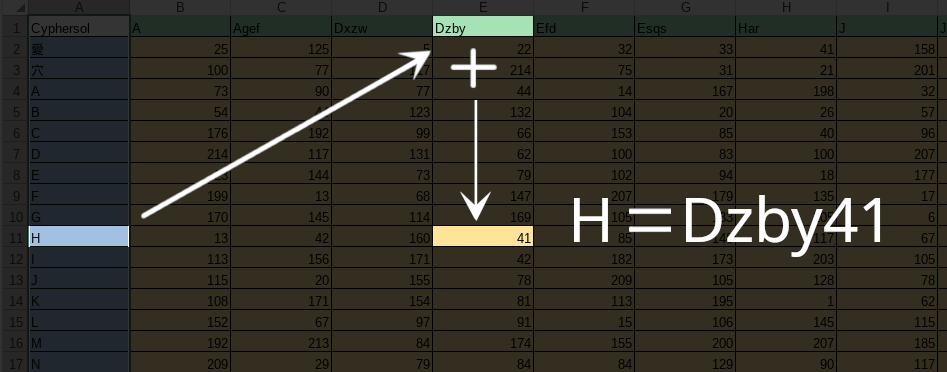
Nehmen wir an, wir möchten den Buchstaben H codieren.
Wir müssen den Inhalt einer Zelle aus Zone A nehmen, und für dieses Beispiel nehmen wir die Zelle aus der Spalte E.
Der Inhalt dieser Zelle ist Dzby.
Sobald dies geschehen ist, müssen wir die Zahl aus derselben Spalte nehmen, die der Zeile des zu codierenden Zeichens, dem H, entspricht, und zwar 41.
Der Code für dieses Zeichen lautet Dzby41 (siehe folgendes Bild).
Nehmen wir an, wir möchten das Wort HELLO codieren.
Wir müssen 5 Großbuchstaben codieren.
Schauen wir uns einige mögliche Ergebnisse an:
Snd206N170Ua150Tg24Qp109
Tg90Nqj124Usr114Esqs106Ua172
Qjhb149Qjhb145K88Tg24J27
V35N170S154Ua150Ua172
Für eine gründliche Überprüfung findest du unten auf dieser Seite Links zum Herunterladen der Matrix sowohl im xlsx- als auch im json-Format.
Sobald du die Matrix hast, erstelle eine Datei mit dem Namen code.txt im cyphersol_data-Ordner, füge die Beispielcodes ein und dekodiere sie mit der App.
All diese Codes sind das Ergebnis des gleichen Wortes HELLO.
In diesem Fall codieren wir ein einzelnes Wort, aber wie wir sehen werden, ist es der Funktion zur Verkettung der Minicodes völlig egal, ob es sich um einzelne einfache Wörter oder um komplexe Sätze mit Sonderzeichen, Satzzeichen, Leerzeichen oder Zeilenumbrüchen handelt.
Jedes Zeichen wird auf die gleiche Weise codiert und verkettet.
Sehen wir uns nun das Ergebnis der ersten von 4 Codierungen des Wortes HELLO an:
Snd206N170Ua150Tg24Qp109
Hier ist das detaillierte Ergebnis der Kodierung der einzelnen Zeichen:
| Zeichen | Verkettung | Code |
|---|---|---|
| H = | Snd + 206 = | Snd206 |
| E = | N + 170 = | N170 |
| L = | Ua + 150 = | Ua150 |
| L = | Tg + 24 = | Tg24 |
| O = | Qp + 109 = | Qp109 |
Dieser Dekodierungsprozess kann auch manuell durchgeführt werden (auch wenn es deutlich länger dauert).
Jedes codierte Zeichen in einem Wort oder Satz beginnt mit einem Großbuchstaben und endet mit der letzten Zahl vor dem nächsten Großbuchstaben.
Im soeben besprochenen Beispiel kann man dies gut erkennen, wenn man sich die verketteten Minicodes anschaut, die durch verschiedene Farben hervorgehoben sind:
Snd206N170Ua150Tg24Qp109
Die manuelle Kodierung und Dekodierung könnte bei den aufmerksamen Lesern unter euch eine Frage aufwerfen.
Es funktioniert gut für Zeichen, aber wie verhält es sich mit der manuellen Kodierung von Leerzeichen und Zeilenumbrüchen?
Ich werde nicht auf die technischen Details eingehen, die es mir ermöglicht haben, die Kodierung und Dekodierung von Leerzeichen und Zeilenumbrüchen auf Software-Ebene zu erreichen (ihr könnt den Code dafür analysieren), aber die Lösung auf Software-Ebene ist auch die Lösung für die manuelle Identifizierung.
Im Wesentlichen bestand die Lösung darin, sowohl dem Leerzeichen als auch dem Zeilenumbruch ein Symbol zuzuweisen.
Genauer gesagt ein Ideogramm.
für Leerzeichen bezieht sich dies auf das Symbol 愛 (Zeile 2 der Matrix)
für Zeilenumbrüche bezieht sich dies auf das Symbol 穴 (Zeile 3 der Matrix).
Lassen Sie uns nun einen Text analysieren, in dem ein Leerzeichen vorhanden ist.
Codieren wir den Satz HELLO WORLD.
Hier ist eines der möglichen Ergebnisse:
Dzby41Esqs94Zuu74Rw179Efd32Y57Qjhb45Wu131Np18Rgdf139
Sehen wir uns zunächst den Minicode Efd32 an.
Er gehört zur Spalte F der Matrix und zum Zeichen 愛, das den Abstand zwischen HELLO und WORLD darstellt.
Die einzige Information, die sich aus einem solchen Minicode ableiten lässt – bei dem jedes Zeichen, Leerzeichen oder jeder Zeilenumbruch eindeutig codiert ist – ist die Anzahl der Zeichen im Satz. Wie viele Wörter enthalten sind, kann man jedoch in keiner Weise erkennen.
Hier ist das detaillierte Ergebnis der Codierung der einzelnen Zeichen und des Leerzeichens:
| Zeichen | Verkettung | Code |
|---|---|---|
| H = | Dzby + 41 = | Dzby41 |
| E = | Esqs + 94 = | Esqs94 |
| L = | Zuu + 74 = | Zuu74 |
| L = | Rw + 179 = | Rw179 |
| O = | R + 109 = | R109 |
| Spazio = | Efd + 32 = | Efd32 |
| W = | Y + 57 = | Y57 |
| O = | Qjhb + 45 = | Qjhb45 |
| R = | Wu + 131 = | Wu131 |
| L = | Np + 18 = | Np18 |
| D = | Rgdf + 139 = | Rgdf139 |
Leerzeichen und Zeilenumbruch
Wie bereits erwähnt, werden sowohl Leerzeichen als auch Zeilenumbrüche genauso codiert wie alle anderen Zeichen.
Wichtig ist zu verstehen, dass sie immer codiert werden.
Wenn ich zwischen zwei Wörtern nur ein Leerzeichen einfüge, wird es einmal codiert.
Wenn ich 10 Leerzeichen einfüge, werden alle mit 10 eindeutigen Minicodes codiert.
Und dasselbe gilt für Zeilenumbrüche, ganz gleich an welcher Stelle sie im Text stehen.
Lade die Beispielmatrix für dieses Tutorial herunter
Auf der nächsten Seite des Leitfadens werden wir verstehen, wie die Dekodierung eines Codes funktioniert.