Qu'est-ce que Cyphersol?
Cyphersol est un système innovant de codage et de décodage, extrêmement polyvalent.
Le système repose sur la division d’un texte à coder en deux éléments distincts et uniques dans chacune de leurs parties.
Pour reconstruire le texte original, il est nécessaire de disposer des deux éléments, car pris séparément ils n’ont aucune utilité.
Grâce à sa structure et à son système de codage, il offre un très haut niveau de sécurité dans différents domaines.
Le système repose sur la division d’un texte à coder en deux éléments distincts et uniques dans chacune de leurs parties.
Pour reconstruire le texte original, il est nécessaire de disposer des deux éléments, car pris séparément ils n’ont aucune utilité.
Grâce à sa structure et à son système de codage, il offre un très haut niveau de sécurité dans différents domaines.
La matrice et le code
Pour encoder un texte avec Cyphersol, il est nécessaire de générer tout d’abord une matrice unique, représentant le premier des deux éléments indispensables.
Ensuite, en utilisant cette matrice, vous obtiendrez le deuxième élément, le code unique.
Ces deux éléments, matrice et code, sont étroitement liés.
Seule la personne qui possède ces deux éléments pourra reconstituer le texte original.
Unicité des matrices et des codes
Les matrices et les codes générés par Cyphersol sont toujours uniques, c’est-à-dire pratiquement impossibles à dupliquer.
La probabilité que deux éléments identiques soient créés est virtuellement nulle.
Les raisons détaillées de cette unicité seront approfondies plus loin.
Cette caractéristique rend les matrices et les codes indéchiffrables et inviolables, garantissant une sécurité maximale.
Ensuite, en utilisant cette matrice, vous obtiendrez le deuxième élément, le code unique.
Ces deux éléments, matrice et code, sont étroitement liés.
Seule la personne qui possède ces deux éléments pourra reconstituer le texte original.
Unicité des matrices et des codes
Les matrices et les codes générés par Cyphersol sont toujours uniques, c’est-à-dire pratiquement impossibles à dupliquer.
La probabilité que deux éléments identiques soient créés est virtuellement nulle.
Les raisons détaillées de cette unicité seront approfondies plus loin.
Cette caractéristique rend les matrices et les codes indéchiffrables et inviolables, garantissant une sécurité maximale.
Le système de codage
Un mot, une phrase, un chapitre de livre — en bref, tout document texte — est composé d’une série d’éléments.
Ces éléments — lettres, chiffres, symboles, espaces, signes de ponctuation et retours à la ligne — sont tous reconnaissables et identifiables, car chacun possède sa propre identité. Et c’est justement grâce à cette identité que nous pouvons lire et comprendre le contenu.
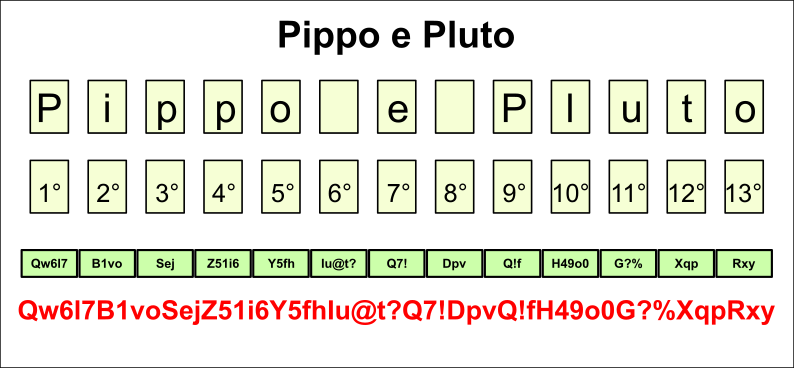
Prenons comme exemple la phrase : Pippo e Pluto
On y trouve :
2 lettres P majuscules,
2 lettres p minuscules,
2 espaces,
et d’autres caractères distincts.
Au total, la phrase est composée de 13 éléments, chacun avec une identité bien précise.
Certaines identités se répètent, comme les deux P majuscules ou les deux espaces.
Maintenant, pour comprendre le fonctionnement du système de codage Cyphersol, essayons de changer de perspective.
Prenons la même phrase, “Pippo e Pluto”, et ignorons complètement l’identité des éléments.
Considérons-les simplement comme 13 positions.
À ce stade, imaginons vider chaque position de son identité originale et la remplir avec une chaîne aléatoire et unique.
Nous obtiendrons ainsi 13 chaînes distinctes, une pour chaque position.
Assemblons maintenant les 13 chaînes, que nous appellerons désormais minicodes.
Le résultat sera un code composé de 13 minicodes uniques, sans aucune référence explicite au contenu original.
Le premier minicode, par exemple, ne représente plus la lettre majuscule “P” : il représente simplement la première position.
Évidemment, il sera lié à la lettre P mais uniquement lors des phases de codage et de décodage, comme nous le verrons plus tard.
Tant qu’il fait partie d’un code, il représente uniquement une position.
Voici le cœur du système Cyphersol :
une transformation dans laquelle chaque élément du texte original est remplacé par une valeur unique, déconnectée de son identité initiale.
Voyons maintenant un exemple pratique d’attribution de minicodes aux 13 positions.
Qw6l7B1voSejZ51i6Y5fhIu@t?Q7!DpvQ!fH49o0G?%XqpRxy
Nous avons compris un concept fondamental :
un code construit avec des minicodes uniques et aléatoires, sans aucune référence directe aux éléments originaux, ne peut pas être déchiffré seul.
Il ne contient aucun indice, ne révèle rien : il est totalement anonyme.
À ce stade, une question naturelle se pose :
Comment sera-t-il possible de reconstruire le texte original ?
La réponse se trouve dans les prochaines étapes du tutoriel.
Le code seul ne suffit pas
Le code est exactement ce qu’il est censé être :
un élément unique et totalement indéchiffrable.
C’est ainsi que le créateur du système Cyphersol l’a imaginé.
Mais le système ne s’arrête pas là.
Il prévoit également une méthode pour reconstruire le texte original, à condition de disposer d’un second élément essentiel.
L’idée derrière Cyphersol est simple et puissante :
Pour reconstruire un texte codé, deux éléments distincts sont nécessaires, chacun dénué de sens pris séparément.
Nous avons déjà parlé du premier élément : le code.
Le second est la matrice.
Qu’est-ce que la matrice
La matrice est un fichier qui contient tous les caractères que le système peut coder :
actuellement 213 symboles, plus l’espace et le retour à la ligne, soit un total de 215 éléments.
Chaque élément de la matrice reçoit, de manière aléatoire, une série de minicodes uniques.
Le nombre de minicodes attribués à chaque élément est choisi par l’utilisateur, en fonction de ses besoins (typiquement selon la longueur des textes à coder).
L’unicité comme garantie
Un minicode :
- apparaît une seule fois dans la matrice ;
- est utilisé une seule fois dans le code.
Cela signifie que chaque minicode est irrépétable, tant dans la matrice que dans le texte codé.
Exemple pratique
Supposons que nous voulions coder la phrase :
"Topolino e Paperino"
Le caractère le plus fréquent est la lettre "o" minuscule, qui apparaît 4 fois.
Pour coder correctement cette phrase :
la matrice doit contenir au moins 4 minicodes ;
s’il n’y en avait que 3, le logiciel ne pourrait pas terminer le codage.
Cela parce que chaque "o" doit être représenté par un minicode différent et unique.
Conclusion
Choisir un nombre plus ou moins élevé de minicodes ne change pas la sécurité du système,
mais détermine la longueur maximale des textes pouvant être codés.
La robustesse de la méthode reste inchangée :
même avec un seul minicode par élément, le code restera indéchiffrable sans la matrice correspondante.
🔐 Phase de codage
Après avoir créé une matrice, l’utilisateur peut procéder au codage d’un texte.
Le logiciel analyse le contenu et assigne aléatoirement les minicodes aux différentes positions occupées par les caractères à coder.
Il est important de souligner que le codage n’est jamais identique :
même avec le même texte et la même matrice, chaque exécution génère un code différent.
Une matrice avec de nombreux minicodes permet de coder un même texte un nombre infini de fois, en produisant à chaque fois un résultat unique.
Les minicodes sont mis en séquence pour former le code final.
Une fois que la matrice et le code sont obtenus, l’utilisateur peut supprimer le texte en clair :
ces deux éléments permettront, plus tard, de reconstruire le contenu.
⚠️ Attention :
Les deux fichiers doivent être enregistrés séparément.
🔓 Phase de décodage et de reconstruction
Pour reconstruire le texte original, l’utilisateur devra :
Placer la matrice et le code dans le dossier de travail de l’application Cyphersol (comme indiqué plus tard).
S’assurer que les deux fichiers sont exactement les mêmes que ceux utilisés lors du codage.
❗ Utiliser une matrice différente de l’originale empêchera toute possibilité de décodage.
À ce stade, l’application :
Analysera le contenu du code ;
Reconnaîtra chaque minicodage et trouvera le caractère correspondant dans la matrice ;
Reconstruira le texte en effectuant un processus inverse de celui du codage.
Le résultat sera le texte original en clair, exactement tel qu’il a été saisi au départ.
🧠 Comment l’app reconnaît les minicodes
Les plus attentifs se demanderont :
"Comment l’app parvient-elle à reconnaître les minicodes individuels dans un long code compact, sans espaces ni séparateurs ?"
La réponse réside dans une caractéristique clé du système Cyphersol, conçue précisément à cet effet.
🔹 Chaque minicode commence par une lettre majuscule, et
🔹 ne peut contenir qu’une seule lettre majuscule.
Cette règle simple mais efficace permet au logiciel d’identifier avec précision où commence et où se termine chaque minicode, même dans un flux de texte continu.
🧬 Unicité du système
Cette structure ne sert pas uniquement au décodage automatique par l’app :
c’est aussi ce qui rend Cyphersol unique par rapport à tout autre système de codage.
💡 En effet, grâce à cette logique, il est possible — pour ceux qui le souhaitent — d’effectuer le codage et le décodage manuellement, sans avoir besoin du logiciel.
Une caractéristique qui offre un niveau supplémentaire de contrôle, de transparence et de sécurité.
🔍 Comment vérifier que les minicodes sont vraiment uniques
Très intéressant, mais une question se pose naturellement :
"Qui nous garantit que les minicodes présents dans la matrice et dans le code sont vraiment uniques ?"
✅ Méthode intuitive : test pratique
Un premier contrôle simple et efficace a déjà été présenté :
Il suffit de créer une matrice en choisissant un petit nombre de minicodes, par exemple 3, puis d’essayer de coder un texte contenant un caractère répété plus de trois fois (ex. la lettre “o” dans la phrase Topolino e Paperino).
Le système refusera la codification, confirmant que chaque minicode ne peut être utilisé qu’une seule fois.
🧪 Méthode avancée : vérification directe avec le terminal
Pour un contrôle complet et rigoureux de l’unicité des minicodes dans la matrice, on peut effectuer une vérification manuelle.
Supposons que nous ayons créé une matrice avec 1000 minicodes pour chacun des 215 caractères codifiables (y compris l’espace et le retour à la ligne).
Nous nous attendons donc à un total de :
1000 minicodes × 215 caractères = 215000 minicodes uniques
🔧 Vérification sur Linux avec le terminal
Assurez-vous d’être dans le répertoire contenant matrix.json
Ouvrez un terminal et tapez les commandes suivantes :
Ces éléments — lettres, chiffres, symboles, espaces, signes de ponctuation et retours à la ligne — sont tous reconnaissables et identifiables, car chacun possède sa propre identité. Et c’est justement grâce à cette identité que nous pouvons lire et comprendre le contenu.
Prenons comme exemple la phrase : Pippo e Pluto
On y trouve :
2 lettres P majuscules,
2 lettres p minuscules,
2 espaces,
et d’autres caractères distincts.
Au total, la phrase est composée de 13 éléments, chacun avec une identité bien précise.
Certaines identités se répètent, comme les deux P majuscules ou les deux espaces.
Maintenant, pour comprendre le fonctionnement du système de codage Cyphersol, essayons de changer de perspective.
Prenons la même phrase, “Pippo e Pluto”, et ignorons complètement l’identité des éléments.
Considérons-les simplement comme 13 positions.
À ce stade, imaginons vider chaque position de son identité originale et la remplir avec une chaîne aléatoire et unique.
Nous obtiendrons ainsi 13 chaînes distinctes, une pour chaque position.
Assemblons maintenant les 13 chaînes, que nous appellerons désormais minicodes.
Le résultat sera un code composé de 13 minicodes uniques, sans aucune référence explicite au contenu original.
Le premier minicode, par exemple, ne représente plus la lettre majuscule “P” : il représente simplement la première position.
Évidemment, il sera lié à la lettre P mais uniquement lors des phases de codage et de décodage, comme nous le verrons plus tard.
Tant qu’il fait partie d’un code, il représente uniquement une position.
Voici le cœur du système Cyphersol :
une transformation dans laquelle chaque élément du texte original est remplacé par une valeur unique, déconnectée de son identité initiale.
Voyons maintenant un exemple pratique d’attribution de minicodes aux 13 positions.
Qw6l7B1voSejZ51i6Y5fhIu@t?Q7!DpvQ!fH49o0G?%XqpRxy
Nous avons compris un concept fondamental :
un code construit avec des minicodes uniques et aléatoires, sans aucune référence directe aux éléments originaux, ne peut pas être déchiffré seul.
Il ne contient aucun indice, ne révèle rien : il est totalement anonyme.
À ce stade, une question naturelle se pose :
Comment sera-t-il possible de reconstruire le texte original ?
La réponse se trouve dans les prochaines étapes du tutoriel.
Le code seul ne suffit pas
Le code est exactement ce qu’il est censé être :
un élément unique et totalement indéchiffrable.
C’est ainsi que le créateur du système Cyphersol l’a imaginé.
Mais le système ne s’arrête pas là.
Il prévoit également une méthode pour reconstruire le texte original, à condition de disposer d’un second élément essentiel.
L’idée derrière Cyphersol est simple et puissante :
Pour reconstruire un texte codé, deux éléments distincts sont nécessaires, chacun dénué de sens pris séparément.
Nous avons déjà parlé du premier élément : le code.
Le second est la matrice.
Qu’est-ce que la matrice
La matrice est un fichier qui contient tous les caractères que le système peut coder :
actuellement 213 symboles, plus l’espace et le retour à la ligne, soit un total de 215 éléments.
Chaque élément de la matrice reçoit, de manière aléatoire, une série de minicodes uniques.
Le nombre de minicodes attribués à chaque élément est choisi par l’utilisateur, en fonction de ses besoins (typiquement selon la longueur des textes à coder).
L’unicité comme garantie
Un minicode :
- apparaît une seule fois dans la matrice ;
- est utilisé une seule fois dans le code.
Cela signifie que chaque minicode est irrépétable, tant dans la matrice que dans le texte codé.
Exemple pratique
Supposons que nous voulions coder la phrase :
"Topolino e Paperino"
Le caractère le plus fréquent est la lettre "o" minuscule, qui apparaît 4 fois.
Pour coder correctement cette phrase :
la matrice doit contenir au moins 4 minicodes ;
s’il n’y en avait que 3, le logiciel ne pourrait pas terminer le codage.
Cela parce que chaque "o" doit être représenté par un minicode différent et unique.
Conclusion
Choisir un nombre plus ou moins élevé de minicodes ne change pas la sécurité du système,
mais détermine la longueur maximale des textes pouvant être codés.
La robustesse de la méthode reste inchangée :
même avec un seul minicode par élément, le code restera indéchiffrable sans la matrice correspondante.
🔐 Phase de codage
Après avoir créé une matrice, l’utilisateur peut procéder au codage d’un texte.
Le logiciel analyse le contenu et assigne aléatoirement les minicodes aux différentes positions occupées par les caractères à coder.
Il est important de souligner que le codage n’est jamais identique :
même avec le même texte et la même matrice, chaque exécution génère un code différent.
Une matrice avec de nombreux minicodes permet de coder un même texte un nombre infini de fois, en produisant à chaque fois un résultat unique.
Les minicodes sont mis en séquence pour former le code final.
Une fois que la matrice et le code sont obtenus, l’utilisateur peut supprimer le texte en clair :
ces deux éléments permettront, plus tard, de reconstruire le contenu.
⚠️ Attention :
Les deux fichiers doivent être enregistrés séparément.
🔓 Phase de décodage et de reconstruction
Pour reconstruire le texte original, l’utilisateur devra :
Placer la matrice et le code dans le dossier de travail de l’application Cyphersol (comme indiqué plus tard).
S’assurer que les deux fichiers sont exactement les mêmes que ceux utilisés lors du codage.
❗ Utiliser une matrice différente de l’originale empêchera toute possibilité de décodage.
À ce stade, l’application :
Analysera le contenu du code ;
Reconnaîtra chaque minicodage et trouvera le caractère correspondant dans la matrice ;
Reconstruira le texte en effectuant un processus inverse de celui du codage.
Le résultat sera le texte original en clair, exactement tel qu’il a été saisi au départ.
🧠 Comment l’app reconnaît les minicodes
Les plus attentifs se demanderont :
"Comment l’app parvient-elle à reconnaître les minicodes individuels dans un long code compact, sans espaces ni séparateurs ?"
La réponse réside dans une caractéristique clé du système Cyphersol, conçue précisément à cet effet.
🔹 Chaque minicode commence par une lettre majuscule, et
🔹 ne peut contenir qu’une seule lettre majuscule.
Cette règle simple mais efficace permet au logiciel d’identifier avec précision où commence et où se termine chaque minicode, même dans un flux de texte continu.
🧬 Unicité du système
Cette structure ne sert pas uniquement au décodage automatique par l’app :
c’est aussi ce qui rend Cyphersol unique par rapport à tout autre système de codage.
💡 En effet, grâce à cette logique, il est possible — pour ceux qui le souhaitent — d’effectuer le codage et le décodage manuellement, sans avoir besoin du logiciel.
Une caractéristique qui offre un niveau supplémentaire de contrôle, de transparence et de sécurité.
🔍 Comment vérifier que les minicodes sont vraiment uniques
Très intéressant, mais une question se pose naturellement :
"Qui nous garantit que les minicodes présents dans la matrice et dans le code sont vraiment uniques ?"
✅ Méthode intuitive : test pratique
Un premier contrôle simple et efficace a déjà été présenté :
Il suffit de créer une matrice en choisissant un petit nombre de minicodes, par exemple 3, puis d’essayer de coder un texte contenant un caractère répété plus de trois fois (ex. la lettre “o” dans la phrase Topolino e Paperino).
Le système refusera la codification, confirmant que chaque minicode ne peut être utilisé qu’une seule fois.
🧪 Méthode avancée : vérification directe avec le terminal
Pour un contrôle complet et rigoureux de l’unicité des minicodes dans la matrice, on peut effectuer une vérification manuelle.
Supposons que nous ayons créé une matrice avec 1000 minicodes pour chacun des 215 caractères codifiables (y compris l’espace et le retour à la ligne).
Nous nous attendons donc à un total de :
1000 minicodes × 215 caractères = 215000 minicodes uniques
🔧 Vérification sur Linux avec le terminal
Assurez-vous d’être dans le répertoire contenant matrix.json
Ouvrez un terminal et tapez les commandes suivantes :
jq -r '.[] | .[]' matrix.json | wc -l
jq -r '.[] | .[]' matrix.json | sort | uniq | wc -l
jq -r '.[] | .[]' matrix.json | sort | uniq | wc -l
📌 Que font ces commandes :
La première commande compte le nombre total de minicodes dans la matrice.
La deuxième commande compte le nombre de minicodes uniques.
Si tout est correct, les deux nombres doivent être identiques.
Exemple :
215000
215000
Pour confirmation supplémentaire, vous pouvez modifier la matrice en y insérant des doublons — disons 5 — et vous obtiendrez un résultat semblable à ceci :
215000
214995
❗ Cela signifie que 5 minicodes sont en double, et donc que la matrice n’est plus valide pour Cyphersol.
Conclusions
Chaque élément est unique
Chaque élément créé par Cyphersol est unique.
La matrice est unique.
Le code est unique, composé de dizaines, centaines ou milliers de minicodes eux aussi uniques.
Il n’existera jamais un seul élément dupliqué.
En pratique, coder un même texte même une infinité de fois donnera toujours des résultats différents.
Le système attribue un minicode unique à chaque lettre (majuscule, minuscule, accentuée ou spéciale), chiffre, symbole, espace et retour à la ligne.
Ce processus transforme tout texte en un seul grand code global, lui aussi unique, pouvant être décodé uniquement à l’aide d’une matrice tout aussi unique.
C’est précisément cette caractéristique qui rend le système totalement sécurisé et inviolable.
La première commande compte le nombre total de minicodes dans la matrice.
La deuxième commande compte le nombre de minicodes uniques.
Si tout est correct, les deux nombres doivent être identiques.
Exemple :
215000
215000
Pour confirmation supplémentaire, vous pouvez modifier la matrice en y insérant des doublons — disons 5 — et vous obtiendrez un résultat semblable à ceci :
215000
214995
❗ Cela signifie que 5 minicodes sont en double, et donc que la matrice n’est plus valide pour Cyphersol.
Conclusions
Chaque élément est unique
Chaque élément créé par Cyphersol est unique.
La matrice est unique.
Le code est unique, composé de dizaines, centaines ou milliers de minicodes eux aussi uniques.
Il n’existera jamais un seul élément dupliqué.
En pratique, coder un même texte même une infinité de fois donnera toujours des résultats différents.
Le système attribue un minicode unique à chaque lettre (majuscule, minuscule, accentuée ou spéciale), chiffre, symbole, espace et retour à la ligne.
Ce processus transforme tout texte en un seul grand code global, lui aussi unique, pouvant être décodé uniquement à l’aide d’une matrice tout aussi unique.
C’est précisément cette caractéristique qui rend le système totalement sécurisé et inviolable.




